How to Solve Kites in Geometry
The sum of the interior angles of a kite is equal to 360. The longer diagonal bisects the pair of opposite angles.

Geometry Kite Examples Youtube
A Kite is a flat shape with straight sides.

. The diagonals of a kite intersect at 90. The area of a kite is half the product of its diagonals. The shorter diagonal divides the kite into two isosceles triangles.
A kite is a quadrilateral shape with two pairs of adjacent touching congruent equal-length sides. Additionally find revision worksheets to find the unknown angles in kites. The sum of the interior angles of any polygon can be found by applying the formula.
High school students learn how to find the indicated vertex and non-vertex angles in a kite determine the measure of angles with bisecting diagonals and solve for x in problems involving algebra as well. This is a demo. 55 Properties of Quadrilaterals Lesson A lesson on the properties of quadrilaterals parallelogram rectangle square rhombus kite trapezoid Geometry Lesson 102 area of trapezoid kite and rhombus video explaining the area of the trapezoid rhombus and kite with examples.
Equip yourself with the Angles in a kite chart for thorough. It has two pairs of equal-length adjacent next to each other sides. There are two basic kite area formulas which can be used depending on which information you have.
How to solve kites in geometry About. Use the following properties of the kite to answer the question as asked in the problem. Each pair is two equal-length sides that are adjacent they meet The angles are equal where the two pairs meet.
2 If the. This geometry video tutorial provides a basic introduction into kites. The perimeter of a kite is equal to the sum of the length of all of its sides.
Therefore our equation becomes. The area of the kite is the sum of the areas of those triangles. Sometimes a kite can be a rhombus four congruent sides a dart or even a square four congruent sides and four congruent interior angles.
We also know the area of the rectangle is. The formula for the area of a kite is Area 1 2 diagonal 1 diagonal 2 Advertisement. From the definition a kite is the only quadrilateral that we have discussed that could be concave as with the case of the last kite.
Two pairs of sides. There are two sets of adjacent sides next to each other that are the same length congruent There is one set of congruent angles. Area of a kite is given as half of the product of the diagonals which is same as that of a rhombus.
Formula for Area of a Quadrilateral. Given diagonal and angle bisector. The sum of the interior angles of any quadrilateral must equal.
A kite is a quadrilateral with two pairs of adjacent congruent sides. If you know two diagonals you can calculate the area of a kite as. Learn to identify kites and trapezoids.
The diagonals of the kite are the height and width of the rectangle it is superimposed in and we know that because the area of a rectangle is base times height. A kite is a quadrilateral with two sets of distinct adjacent congruent sides. It looks like the kites you see flying up in the sky.
It explains how to calculate the area of a kite using the length of its two diagonals. Given rectangle and equal segments. That means a kite is all of this.
An online calculator to calculate the sides area perimeter and angles in a kite given its diagonals and distance A O. To find the area of a kite multiply the lengths of the two diagonals and divide by 2 same as multiplying by 12. Diagonals dashed lines cross at right angles.
Up to 10 cash back The area of a kite is half the product of the diagonals. Up to 10 cash back Explanation. If a kite is concave it is called a dart.
The diagonals of a kite are perpendicular. It often looks like. Area e f 2 where e and f are kite diagonals If you know two non-congruent side lengths and the size of the angle between those two sides use the formula.
These are opposite of each other and are between sides that are different lengths. The kite formulas are first given. 1 If the problem is asking for congruent angles identify the pair of non-vertex angles.
Area 12 diagonal 1 diagonal 2. Consider for example a kite with diagonals measuring 6 cm and 4 cm. A kite is symmetrical about its main diagonal.
We define the length of segments A C B D and A O using small letters as follows. Ad Over 27000 video lessons and other resources youre guaranteed to find what you need. Degrees where is the number of sides in the polygon.
Substituting this value in we get the following. Here ACD DCB and ADC CDB. Play full game here.
By definition a kite is a polygon with four total sides quadrilateral. A C e B D f and A O g. Area of a kite can be expressed by the formula.
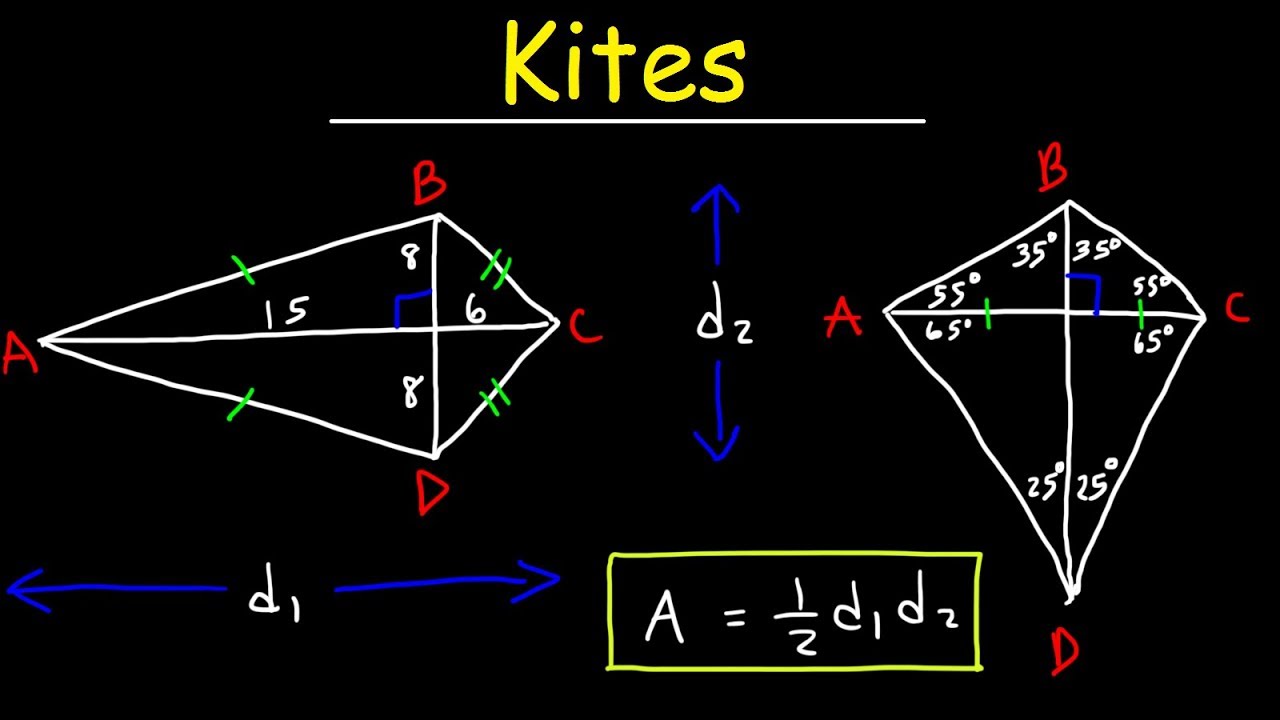
Kites Basic Introduction Geometry Youtube
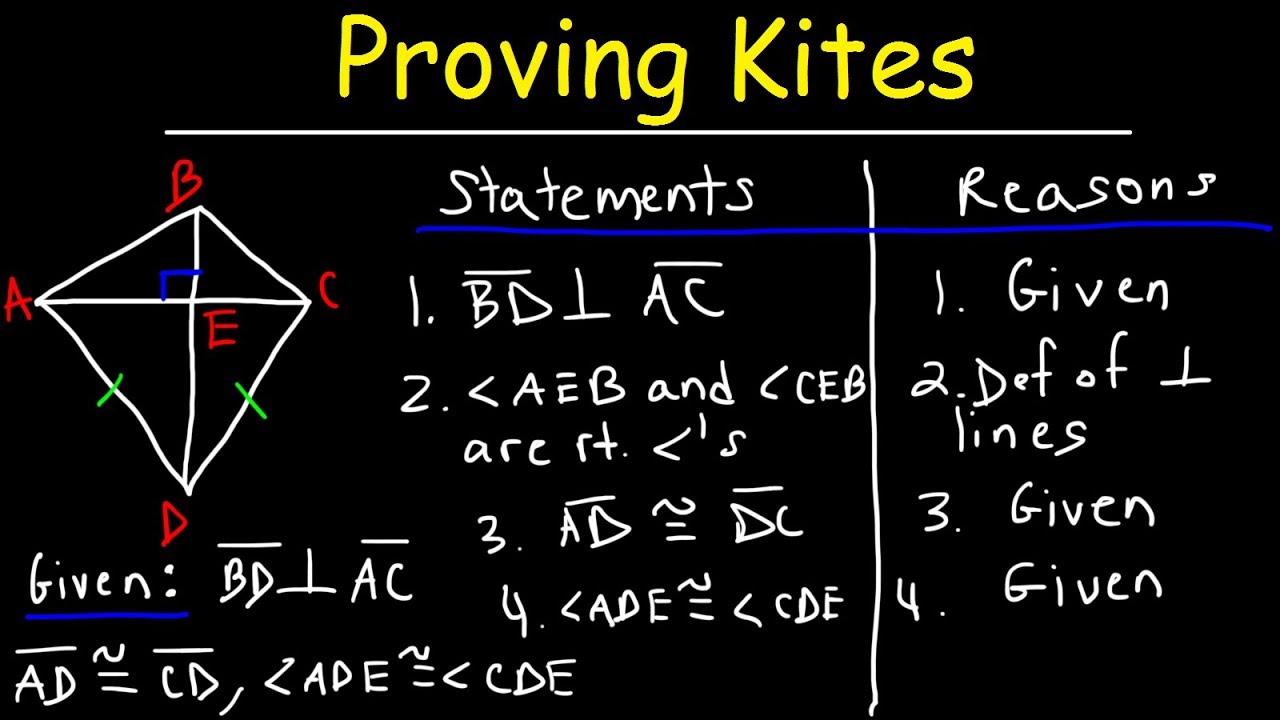
Kites Basic Introduction Geometry Youtube

Question Video Finding The Side Length Of A Kite Given Its Diagonal Lengths Nagwa
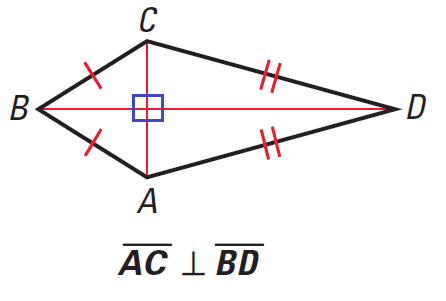
No comments for "How to Solve Kites in Geometry"
Post a Comment